In case you’re new to CrossFit, let me take a minute to bring you up to speed. The CrossFit Open is made up of five workouts, announced weekly over five weeks, usually beginning around mid to late February.
This year, the format is shifting so that moving forward, the Open will take place in October. Read about changes to the CrossFit Games season here.
“The Open” is just the beginning portion of The CrossFit Games® (a series of events to find the fittest athletes on earth). Anyone can join (I highly encourage that you do) – and you do not have to belong to an affiliate to participate.
Since 2011, we’ve seen tremendous participation growth across The Open:
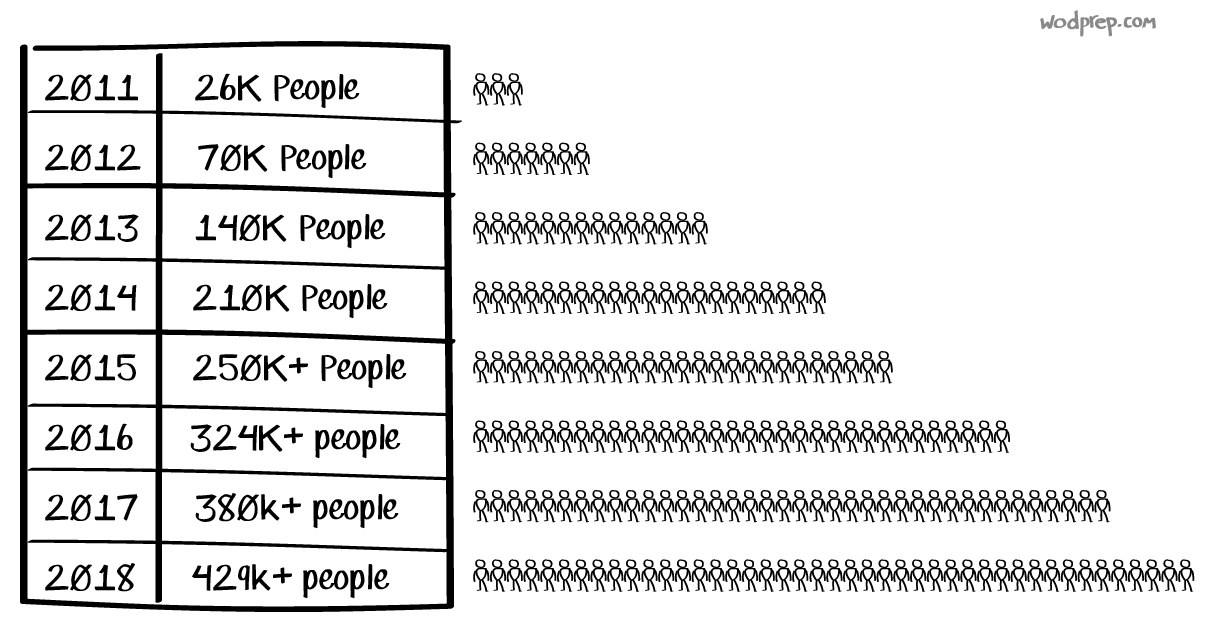
2011 – 2014, 2015, 2016, 2017 – sources
Hacking The 2019 CrossFit Open: Movement Awareness Is Key
Given the many movements within the realm of CrossFit, there is virtually no limit to the combination of movements and rep schemes that can make up a WOD. This simple notion is what keeps athletes coming back for more: “Constantly varied functional movements performed at relatively high intensity”.
Is it possible to master each crossfit movement? While there are many athletes who excel in particular functional fitness movements, the good news is:
We don’t need to perfect every movement under the sun to perform well in the Open.
Due to the nature of the Open, many movements are eliminated because they are difficult to standardize / judge. So far in the early stages of the competition, judging has relied on movements that have binary results such as chest-to-bar-pull-ups.
This is why over 9 years and , we’ve only seen 23 different exercises, 5 of which have been repeated each and every year.
If your chest hits the bar, that’s a rep. If it doesn’t, that is a no-rep.
46 workoutsThese movements are the simplest movements to judge.
The 2019 CrossFit Open: Movements To Focus On
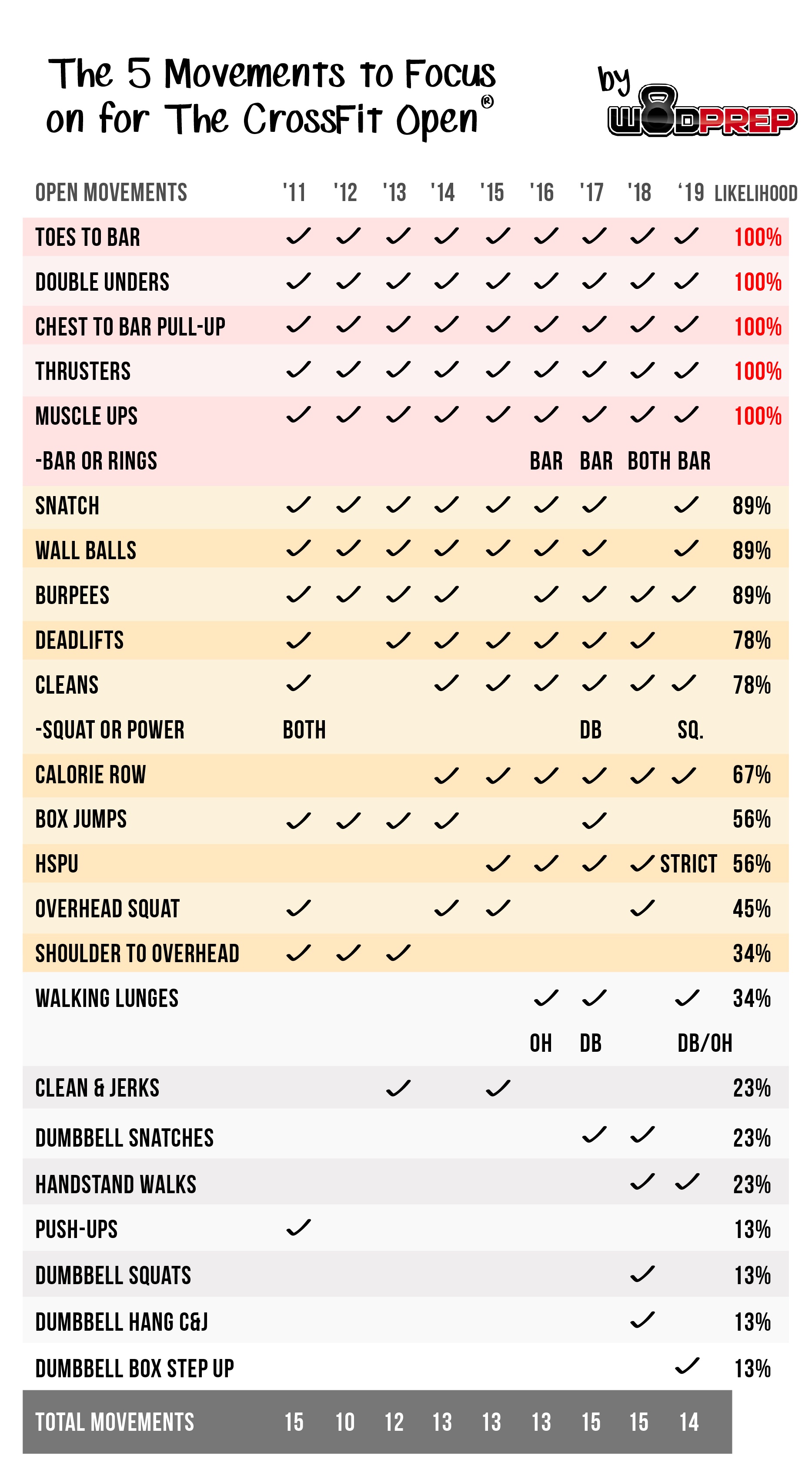
Caption: adapted from Beyond the Whiteboard’s 2017 Graphic
Out of 23 total movements listed, only 5 present themselves each and every year. It is said that history is the greatest indicator of the future. Armed with that knowledge, I highly recommend you keep these movements in mind as you prepare for the 2019 October CrossFit Open.
Take your performance, and CrossFit® skills to the next level. Join the WODprep Academy Today!
Don’t know where to start? Looking to fine tune some of the movements and get ‘Open Ready?’ WODprep is here to help, check out the list of movements below, with links to free guides.
Open Movements (number of times seen, in order):
- Double Unders – 9
- Muscle Ups (bar or ring) – 9
- Toes To Bar – 9
- Thrusters – 9
- Chest To Bar Pull Ups – 9
- Snatch (Full / Power) – 8
- Wall Balls – 8
- Burpees (any kind) – 8
- Deadlifts – 7
- Cleans (Power/Full/DB) – 7
- Calorie Row – 6
- Box Jumps – 5
- HSPU – 5
- Overhead Squats – 4
- Shoulder To Overhead – 3
- Walking Lunges – 3
- Clean and Jerks – 2
- Handstand Walks – 2
- Dumbbell Snatches – 2
- Push Ups – 1
- DB Hang Clean & Jerk – 1
- DB squats – 1
- DB box step-ups – 1
2019 CrossFit Open: The Two Most Important WOD Schemes
The most popular WOD scheme seen in The Open is a couplet, seen 23 times so far – followed by the triplet.
Trendspotting:
While you now have the top crossfit movements that are consistently programmed in the back of your mind, let’s take a minute to look at two trends from the past few years:
- Calorie Row: This guy has attended The Open 67% of the time. However, it’s important to note that the calorie row has shown up every year for the past 6 years straight. It’s an easy way for them to throw some pure cardio into a workout, since running is much harder to standardize, measure, and judge.
- HSPU’s: These fall into this same category as the calorie row. Don’t overlook handstand push-ups just because of their 56% historical attendance rate in the Open. We’ve seen this movement for the past 5 years running (in this most recent Open – strict HSPU), and I wouldn’t be surprised if that trend continues.
Last year we saw Handstand Walks make their first ever debut in the Open, and they showed up again this February Open. I wouldn’t be surprised if we see them again in this 2019 October Open. The good news? We’ve have a great blog post that can help out your Handstand Walking.
How Can I Perform Better In The CrossFit Open?
1. Find the easy wins.
Since we now know the movements that are highly likely to be included in this year’s Open, let’s shift our focus there. Which one of those movements is your biggest weakness? If you are inefficient in any of these seven movements, persistently practicing one of them can significantly improve your score. Thankfully, we have Free Guides for 5 of those top movements to help you get started!
2. Be happy with good enough.
Let’s say you can do 50 double-unders unbroken. Most WODs rarely call for more than 25-40 double unders at a time. Given the fact that you can do 50 unbroken, you are more than likely able to do sets of 25-40 with ease. There is no reason to continue “practicing” double unders at this point. Reduce training of that movement and shift gears to another roadblock movement that you may have.
3. Reduce time on rest & transition.
Since we know 85% of Open workouts are couplets and triplets, we can be sure a lot of time will be spent simply transitioning from one movement to another. In the world of a competition with more than 350K athletes, every tenth of a second counts! Be sure to set up your equipment in a compact environment. Try to limit your rest between movements to zero. The time spent “salsa dancing” in front of a barbell, taking sweet time getting strapped into a rower, or staring up at the pull up bar before your first rep does irreparable damage to your final score.
As in life, the first step is the hardest, so get it out the way as fast as possible! Even if it means just one rep. Furthermore, try to limit your break time within a set to a predetermined number (i.e.: 7 seconds on the clock or 5 slow and controlled breaths). If you need to let go of the pull up bar, or find yourself doing singles late in the WOD, commit yourself to a certain break.
Lastly, be mindful about taking care of your body these next 6 weeks leading into the Open. Eat well, hydrate well, and be proactive about mobility, stretching, and stabilization drills.
Comment below with a BRAND NEW movement you’re expecting to see in this 2019 October Open.
Good luck!
Other interesting notes about the CrossFit® Open:
- In 2011, The Open consisted of six workouts.
- 15.1 / 15.1A was the first time a workout was separated into two parts.
- Singlet: 11.3 was listed as two movements but it was Clean then Jerk so we categorized it as a single movement for the purposes of this post.
- There were two Single Movement workouts in 2012: AMRAP in 7 min Burpees & then a Snatch Ladder. The 4th & Final Singlet was 15.1A (1RM Clean & Jerk)
- Quintuplet: 14.4 was the only workout which had five movements (Calorie Row, Toes To Bar, Wall Balls, Cleans, & Muscle Ups)
Disclaimer: WODprep is not associated with CrossFit® in any way and these opinions are separate from the CrossFit® brand.
Read More 2026 CrossFit® Quarterfinals Workouts & Strategy
Read More 2026 CrossFit® Open Workouts & Strategy
- 26.3 CrossFit® Open Workout and Standards
- 26.3 CrossFit® Open Strategy and Tips
- 26.2 CrossFit® Open Workout and Standards
- 26.2 CrossFit® Open Strategy and Tips
- 26.1 CrossFit® Open Workout and Standards
- 26.1 CrossFit® Open Strategy and Tips
Read More 2026 CrossFit® Open Content:
- 2026 CrossFit® Open Predictions: What Movements Will We See?
- 5 Bold Predictions for the 2026 Open (Burpees Not Included)
- How to Crush the 2026 CrossFit® Open: Your 4-Day Game Plan
- How to Prepare for the 2026 CrossFit® Open (With Less than 3 Weeks Left!)
- 7 Movements You MUST Master for the 2026 CrossFit® Open
- The 2026 CrossFit® Open Leaderboard: How to Track Your Spot (And Make the Cut)
- The Quarterfinals Are Back: Your Complete Guide to the 2026 CrossFit® Season
Frequently asked questions
What 7 movements should I focus on before the CrossFit® Open?
The recurring Open movements are toes-to-bar, chest-to-bar pull-ups, bar and ring muscle-ups, double-unders, handstand push-ups, and barbell cycling – specifically the clean and snatch. Nail these and you’ll be competitive in virtually any Open workout that comes up.
How early before the Open should I start skill work?
At least 8–12 weeks out for skills you don’t currently have. That’s enough time to build genuine capacity rather than just getting lucky on a single rep. If you have 16+ weeks, even better – focus on one skill at a time rather than spreading your practice across all of them simultaneously.
Which Open movement gives athletes the most trouble?
Ring muscle-ups consistently separate fields more than anything else. They require strength, skill, and coordination simultaneously – if you’re missing any one of those three, the rep doesn’t happen. Toes-to-bar at high volume is the other movement most athletes underestimate.
Is it worth learning bar muscle-ups if I already have ring muscle-ups?
Yes. Bar muscle-ups require a different technique – especially the hip-to-bar pull and the turnover – so having ring muscle-ups doesn’t automatically transfer. The Open has used both, so if you want to be prepared, train both. Bar muscle-ups are generally harder for ring-dominant athletes than the reverse.
How many double-unders should I be able to do unbroken for the Open?
Aiming for 50+ unbroken is a solid benchmark before the Open. Many Open workouts program double-unders in sets of 50–100, and tripping at 20 every set will cost you significant time. If you can’t consistently hit 30 unbroken, that’s your most impactful skill to fix first.